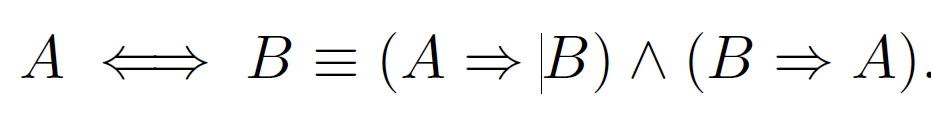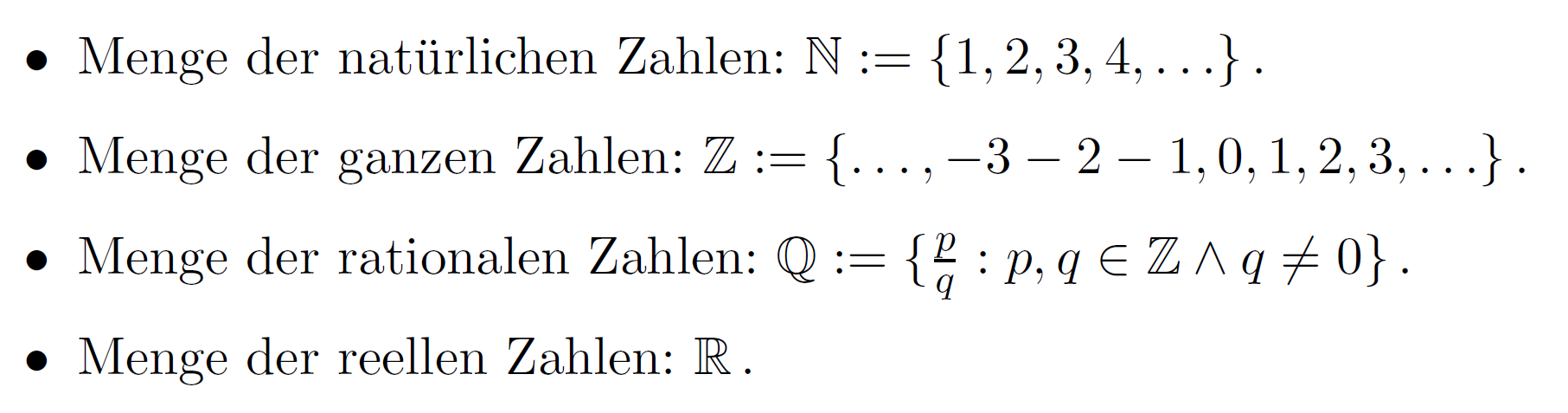Aussagenlogik
In der Aussagenlogik versteht man unter einer Aussage einen sprachlichen oder formalen Ausdruck, dem man genau einen der beiden möglichen Wahrheitswerte (w: wahr, f: falsch) zuordnen kann.

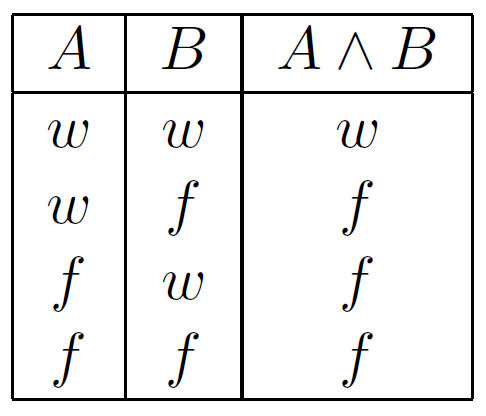
Konjunktion
Disjunktion
Nur F - F ist wirklich falsch.
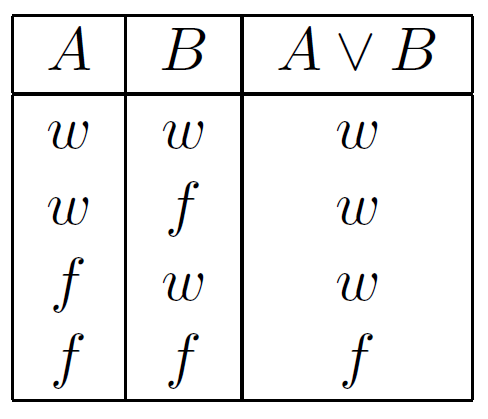
Antivalenz / XOR
Nur dann wahr, wenn nur eins von $A \oplus B$ richtig ist
| A | B | $A \oplus B$ |
|---|---|---|
| W | W | F |
| W | F | W |
| F | W | W |
| F | F | F |
Negation
Disjunktive Normalform
Wahrheitstabelle zu Aussage aufschlüsseln. Jede Teilaussage muss dabei wahr sein und kann dann mit den anderen Teilaussagen über eine Disjunktion verknüpft werden.
Kanonisch disjunktive Normalform
Jede Variable kommt genau einmal vor.
Tautologien
Wenn alle Werte der Aussage wahr sind, unabhängig von den Werten der Variablen.
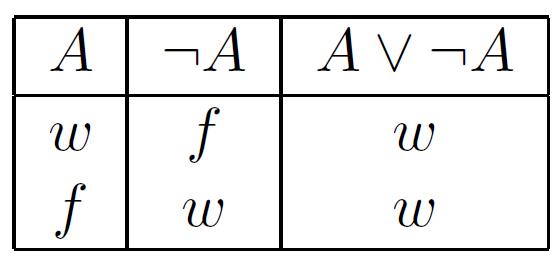
Kontradiktionen
Wenn egal welcher Wert die Variablen haben, die Aussage immer Falsch ist.
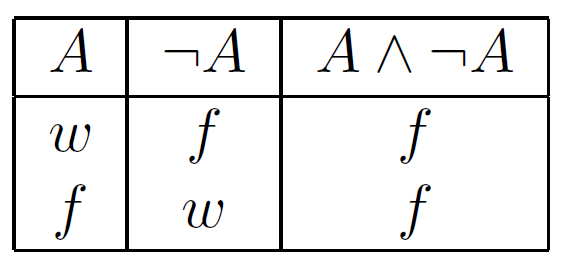
Logische Äquivalenz
Wenn zwei Aussagen die exakt gleiche Wahrheitstabelle haben. P(A, B, ...) $\equiv$ Q(A, B, ...)
Implikation
Ein Element verursacht ein anderes. Wenn A dann folgt B.
![![ [Pasted image 20231015132040.png]]](https://docs.lucanoahcaprez.ch/uploads/images/gallery/2023-10/scaled-1680-/pasted-image-20231015132040.png)
Zusammenhang
Wirkung zwischen Implikation, Umkehrung und Kontraposition.

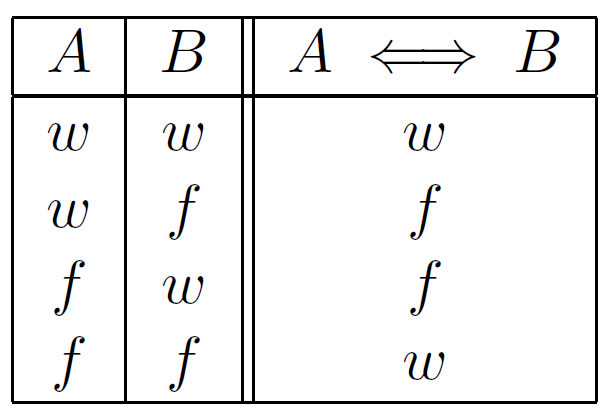
Äquivalenz
Gegenseitige Implikation der Inhalte.
Andere Schreibweise
Aussageformen
Zahlenmenge
Operanden
x $\in$ $\mathbb{R}$ -> Definitionsbereich der Variable x. 3|n -> n ist ein Teiler von 3.
Quantoren
$\forall$ -> Allquantor für alle Elemente. $\exists$ -> Existiert mindestens ein Element.
Negation Existentaussage
$\exists x \in D : P(x) \equiv \forall x \in D: \lnot P(x)$ Entsprechend kann es so umgekehrt werden: $\lnot(\exists x \in D : P(x)) \equiv \forall x \in D: \lnot P(x)$
Negation Allaussage
$\lnot(\forall x \in D: P(x)) \equiv \exists x \in D: \lnot P(x)$
Beweistechniken
Indirekter Beweis
Implikation ist logisch äquivalent zu Kontraposition: $A \implies B \equiv \lnot B \implies \lnot A$ Manchmal einfacher zum Beweisen ist die Kontraposition.
Beweis durch Widerspruch
Hypothese:
$\lnot A \implies B$
Ergibt einen Wirderspurch mit der wahren Aussage:
$\lnot A \implies \lnot B$
Aussagenlogik vs Mengenlehre
Aussage: $x \in A$
Mengenangabe: $A \cap B$

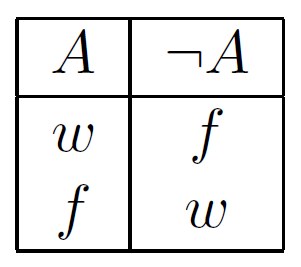
![![[Pasted image 20231015100429.png]]](https://docs.lucanoahcaprez.ch/uploads/images/gallery/2023-10/scaled-1680-/pasted-image-20231015100429.png)