Mengenlehre

Mengen: Grossbuchstaben; A, B, C, ... Elemente: Kleinbuchstaben; a, b, c, ... $p \in A$ Negation: $p \notin A$

Aufschreibearten

Alle Elemente auflisten: $A = a, b, c, x, y, z$ $B = 1, 2, 3, 4$ $C = 1, 2, a, b, c$

Eigenschaften festlegen: $B = n : n \in Z \land n > 5$ B ist die Menge der Elemente n; wofür gilt, n ist eine ganze Zahl grösser als 5.

Extensionalitätaxiom

Zwei Mengen A und B enthalten selbe Elemente. $A = B$ Negation: $A \neq B$

Leere Mengen

Bezechnung: $\emptyset$ Elemente der betrachteten Menge => Universalmenge

Teilmengen

A & B sind zwei Mengen Wenn alle Elemente von A auch in Element B: $A \subseteq B$ Falls keine Teilmenge: $A ⊈ B$

Verneinung

Alle Elemente von A und B: $A \cup B$ $A \cup B := x : x \in A \lor x \in B$

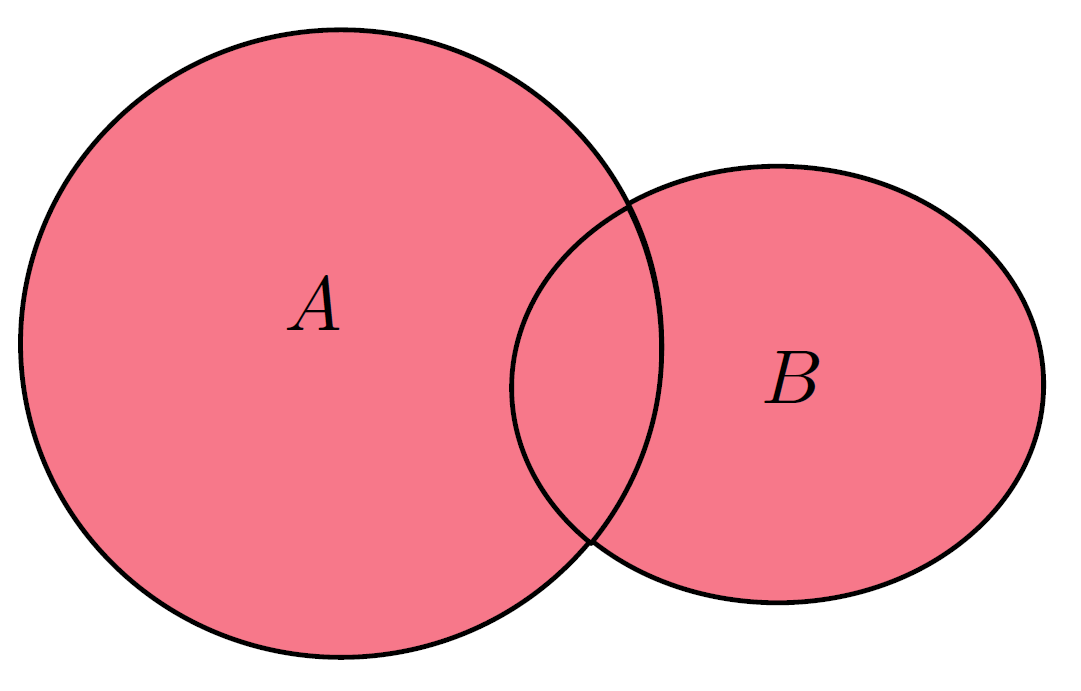
Durchschnitt

Nur Elemente in beiden Mengen: $A \cap B$ $A \cap B := x : x \in A \lor x \in B$ ![[Pasted image 20231024102057.png]]

Disjunktion

Wenn der Durchschnitt zweier Mengen A und B leer ist: $A \cap B = \emptyset$

Komplement

$A \subseteq U$ kann auch als $A^{C}$ geschrieben werden $A^{C} := x : x \in U \lor x \notin A$ ![[Pasted image 20231024102358.png]]

Differenz

Wenn Differenz zwischen A und B ist alles in A, was nicht zu B gehört: $A ∖ B$ $A ∖ B := x : x \in A \land x \notin B$ ![[Pasted image 20231024102640.png]]

Potenzmenge

Alle Teilmengen eines Mengensystems: S = {1, 2} $P (S) = \emptyset, 1, 2, 1, 2$ N Elemente enthalten: $2^{n}$ Elemente.

Partition

Aufteilung in nicht leere Teilmengen, zB. Partition A von S -> $A_{i}$ . Dabei gilt:

Teilmengen $A_{i}$ verschieden von $\emptyset$
Alle $A_{i}$ ergeben S
Paarweise disjunktiv; $A_{i} \cap A_{:} j = \emptyset$ , falls $i \neq j$

Geordnete Paare

Bei Elementen einer Menge spielt die Reihenfolge keine Rolle: $a, b = b, a$ Bei geordneten Paaren hingegen gilt die Reihenfolge zwingen. $(a, b) = (c, d)$ Diese sind nur dann gleich wenn: a = c und b = d

Kartesisches Produkt

Menge aller geordneten Paare (x, y) mit $x \in A$ und $y \in B$ . Bezeichnung: $A \times B$ $A \times B := (x, y) : x \in A \land y \in B$

n-Tupel

Bestehend aus n geordneten Elementen $(a_{1}, a_{2}, a_{c}, \dots, a_{n})$ Zwei n-Tupel sind genau dann gleich: $a_{1} = b_{1} \land a_{2} = b_{2} \land a_{3} = b_{3} \land \dots \land a_{n} = b_{n}$ Bei folgenden Mengen $A_{1}, A_{2}, . . ., A_{n}$ bezeichnen Mengen aller n-Tupel $(a_{1}, b_{2}, . . ., c_{n})$ mit der folgenden Eigenschaft $a_{1} \in A_{1}, a_{2} \in A_{2}, . . ., a_{n} \in A_{n}$ diese Menge $A_{1} \times A_{2} \times . . . \times A_{n}$

Endliche Mengen

Endlich bedeutet, dass die Menge m (natürliche Zahl) verschiedene Elemente hat. Anderfalls ist die Menge unendlich. Bezeichnung der Anzahl Elemente der Mengen: $| A |$ Wenn A und B endliche Mengen sind, dann ist $A \cup B$ ebenfalls enldich: $| A \cup B | = | A | + | B | - | A \cap B |$

Einschluss-Ausschluss-Formeln

![[Pasted image 20231024155838.png]]