Funktionen

Eine Grösse y ist von einer anderen Grösse x abhängig. f(x) -> Bild von x

Urbild

Wenn $y \in B$ dann ist $x \in A$ mit f(x) = y. $y \in B$ kann kein, genau ein oder mehrere Urbilder haben.

Definitionsbereich

Menge A der Funktion f.

Zielbereich

Menge B der Funkction f.

Bild der Funktion f

Die Menge aller Elemente y denen ein x zugeordnet wird. $f(x) = f(A) = { f(x):x \in A } \subset B$ Bild von x unter der Funktion f.

Graph einer Funktion

Der Graph G(f) der Funktion f ist die Menge $G(f) = {(x, f(x)) : x \in A} \subset A \times B$

Abrundungsfunktion

Ordnet jeder reellen Zahl x die grösste ganze Zahl zu. -> 4.154 -> 4

Aufrundungsfunktion

Ordnet jeder reellen Zahl die kleinste ganze Zahl zu. -> 4.154 = 5

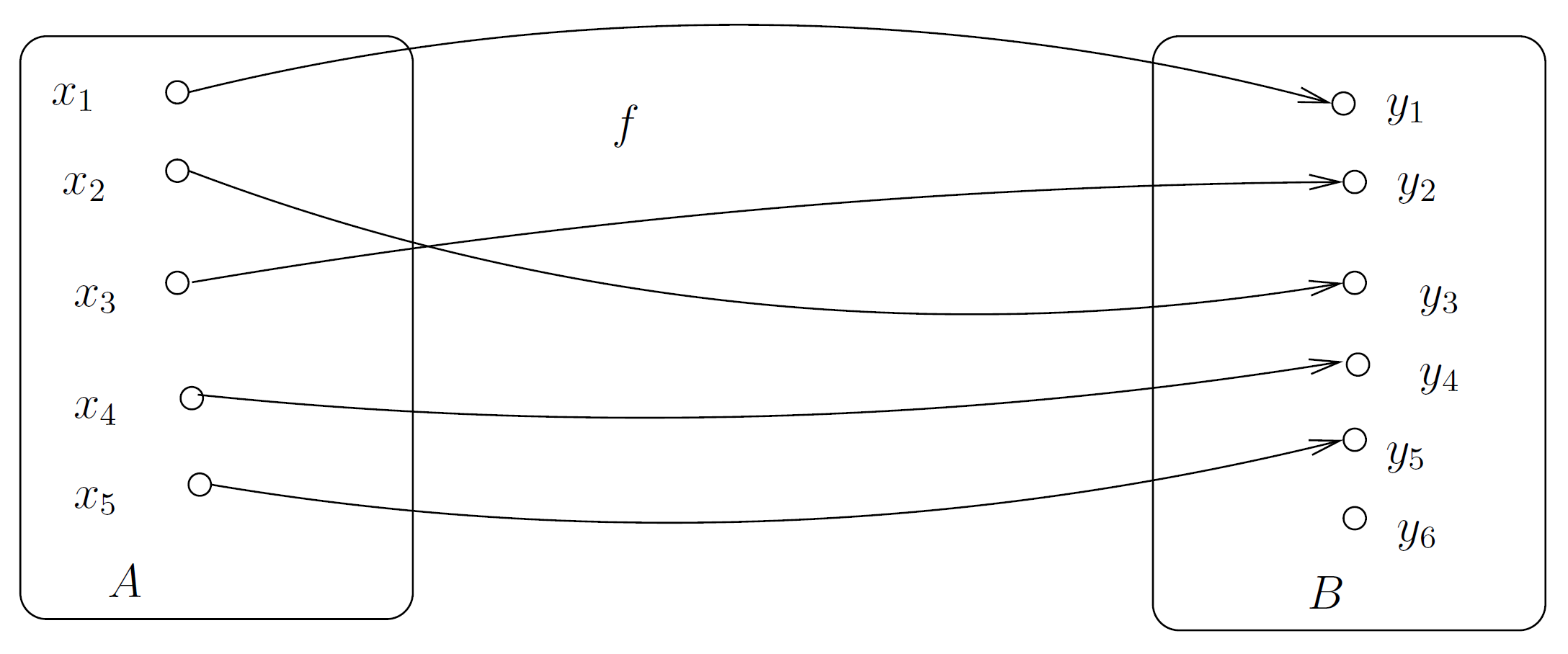
Injektion

x = f(x) ist injektiv wenn: $x_{1} \not = x_{2} \implies f(x_{1}) \not = f(x_{2})$ Jede Funktion schneidet nur einmal eine horizontale Gerade.

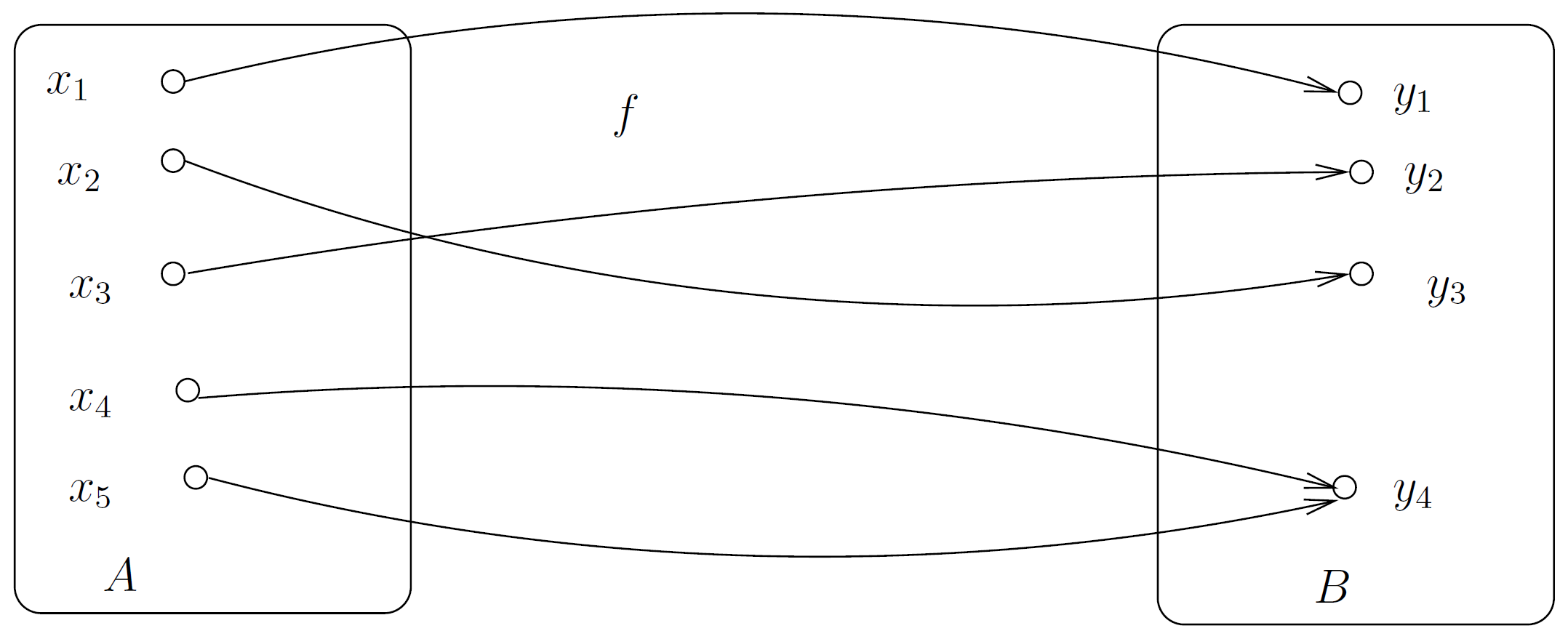
Surjektion

Falls jedes Element des Wertebereichs mindestens ein Urbild besitzt. Wenn jedes $y \in B$ ein $x\in A$ besitzt.

Bijektion

Wenn f injektiv und surjektiv ist. Jedes $y \in B$ besitzt genau ein Urbild.

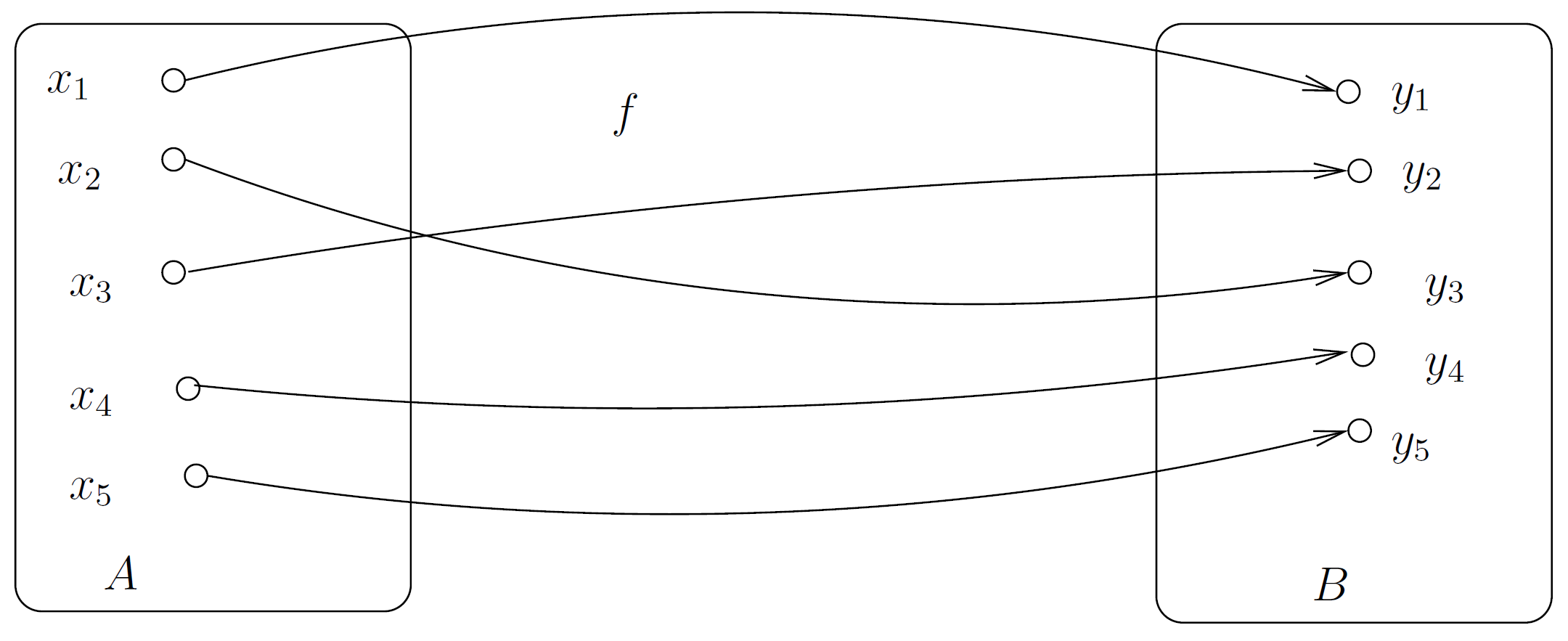
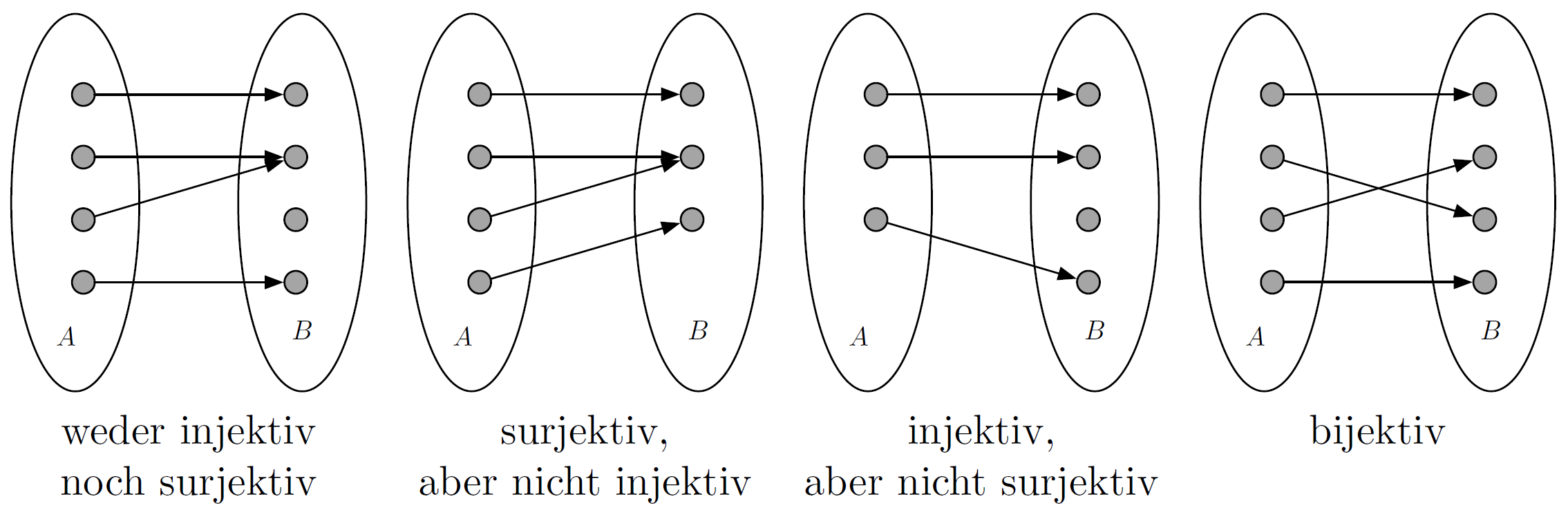
Übersicht injektiv, surjektiv, bijektiv

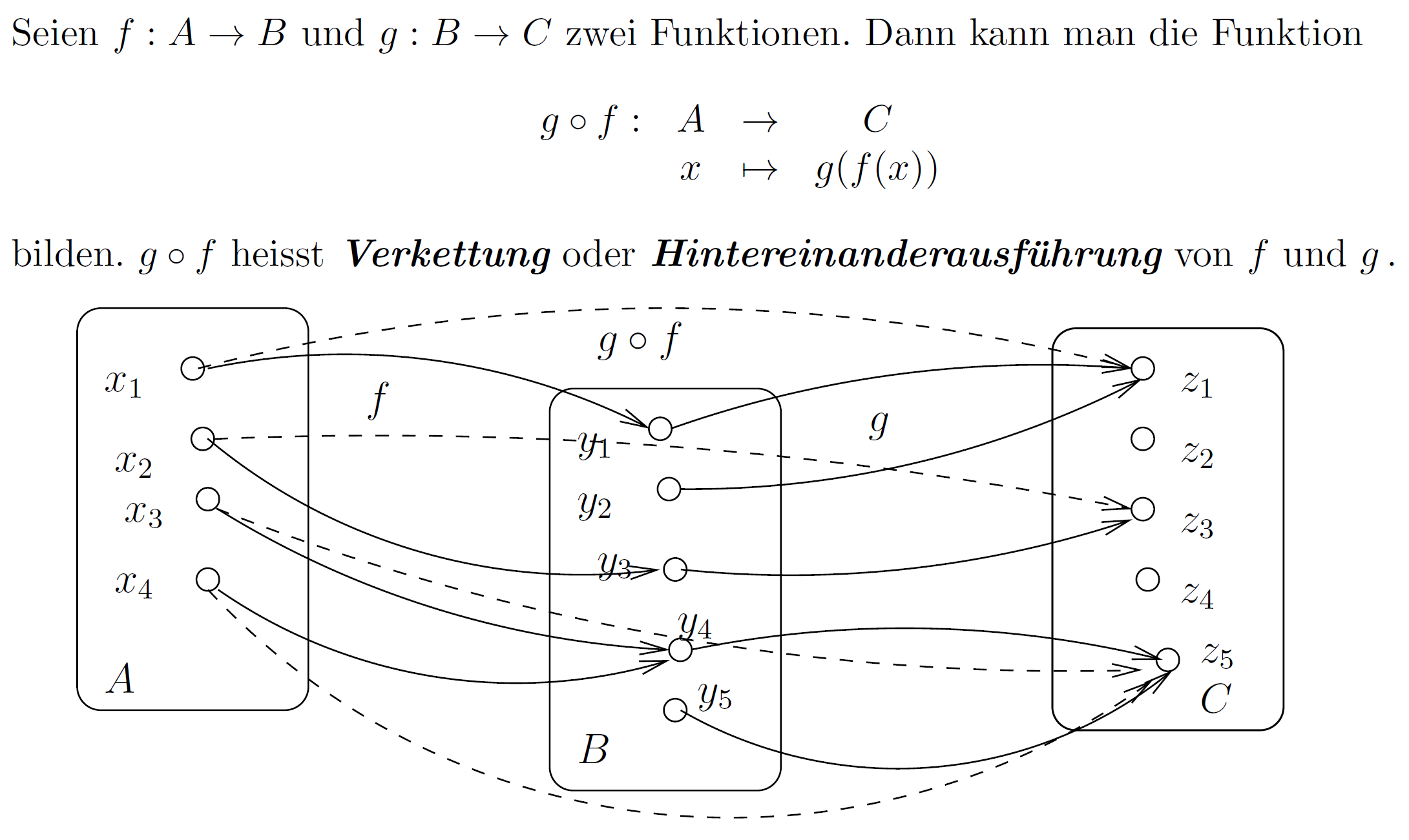
Verkettung

Umkehrfunktion

Wenn f(x) eine biijektive Funktion ist, existiert zu jedem $y \in B$ genau ein $x \in A$ mit f(x) = y. Dies wird auch inverse Abbildung genannt.

Inverse Abbilung

$f(x) -> f^{-1}(x)$ Für jedes $x \in A$: $(f^{-1}\circ f) (x) = f^{-1}(f(x))=x$ Die Umkehrfunktion setzt die Änderungen der Funktion zurück. Wenn eine Funktion invertierbar ist, ist klar, dass sie bijektiv ist.

Mächtigkeit

Anzahl Elemente einer Menge. Gleichmächtig bedeutet |A| = |B|, wenn eine Bijektion zwischen A und B existiert.

Es gibt Teilmengen, die gleichmächtig zur gesamten Menge sind.

Eine Menge M heisst endlich & abzählbar, wenn es eine echte Teilmenge von M gibt, die sich bijektiv auf M abbilden lässt.

Die Menge der reellen Zahlen ist nicht mehr abzählbar: 0.24999... = 0.25 sind gleichmächtig. Das nennt man auch überabzählbar.